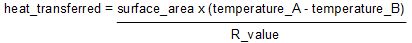Heat transfer/loss formula and how to calculate it

Heat can move, transfer, through material by conduction. In most cases this is considered a loss. The following calculator and examples show how to compute the amount of heat transfer/loss.

Heat transfer/loss calculators

How heat transfer is calculated

(Examples for solar air heaters, houses and underground tanks are given below.)

where:

• heat_transferred is the amount of heat transferred, either lost or gained, through the material separating both sides (BTU / hour)
• surface_area is the surface area of the material separating the two areas that are at different temperatures, it's the material that the heat is being transferred through (Examples: wall, window) (ft²),
• temperature_A is the larger of the two temperatures on both sides of the separator (F),
• temperature_B is the smaller of the two temperatures on both sides of the separator (F),
• R_value is the R-value of the separating material (ft² x F x hours / BTU).

The R-value is the resistance to the movement of heat through the separating material, a house wall in the diagrams on the right. So the formula is saying, get the difference in the temperatures on the two sides of the wall and divide it by the resistance to heat flow through the wall. Once you've done that, multiply it by the area of the wall since the heat is being transferred everywhere on the wall, not just at one location.

In the second example on the right we've significantly increased the wall's R-value, the resistance to heat transfer, from 14 to 28. The effect was to slow down heat loss from 228 BTU per hour to 114 BTU per hour, a major improvement. BTU is a measure of energy.

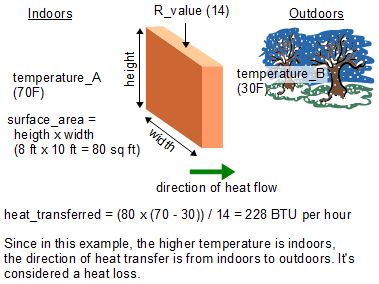
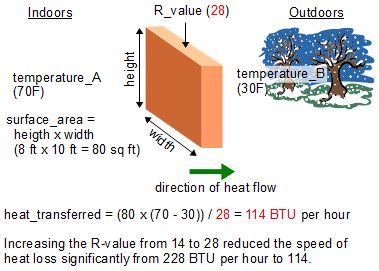
Note that the direction of heat flow is from the higher temperature side to the lower temperature side. Since the formula is subtracting the two temperatures, it's clearer if you use the higher temperature for temperature_A otherwise you'll end up with a negative result, which may be confusing to some.

Examples of heat transfer/loss calculations

Solar heater glazing

The interesting thing when looking at these, especially in the solar heater case, is the difference the two temparatures make. On the left below is a screen solar air heater where the input air moves between the absorber and the glazing before being heated as it passes through the absorber and reenters the house. That means the air between the absorber and the glazing starts out at room temperature and consists of a constant inflow of room temperature air, though it does get heated either by contacting the absorber but not going through it or by radiation from the absorber.

On the right below is a backpass solar air heater such as a downspout one. In that case the air between the absorber and the glazing is never refreshed and increases in temperature from contact with the absorber. This means, theoretically it reaches higher temperatures and so has greater heat loss through the glazing.

More about the different types of solar air heaters can be found on solar air heater types page.

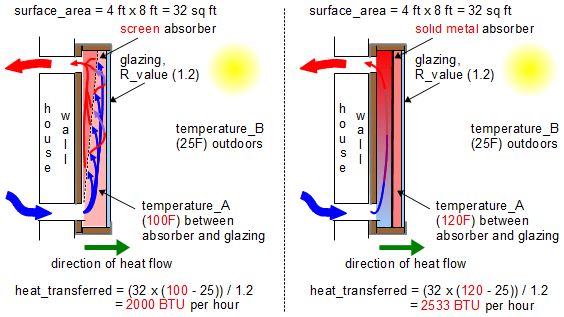
Note that the above conclusions regarding what happens in the two types of collectors are theoretical and do not take into account the many other variables. The intention is only to highlight the affects of a larger temperature difference.

House window with solar air heater

An interesting example of heat loss through a house window is found when people put solar air heaters inside their house directly behind a window as in the ilustration below. In both cases the same amount of solar energy enters the window. Without a solar air heater, the solar energy is absorber/converted to heat by the furniture. With a solar air heater the solar energy is still converted to heat but results in higher temperature air next to the window. This cause a greater rate of heat loss at the window.

Assuming a window R-value of 2, and a window area of 6 square feet, the heat loss with the solar air heater is 321 BTU per hour ([6 x (130 - 23)] / 2). For the window without the solar air heater the heat loss is 150 BTU per hour ([6 x (73 - 23)] / 2).

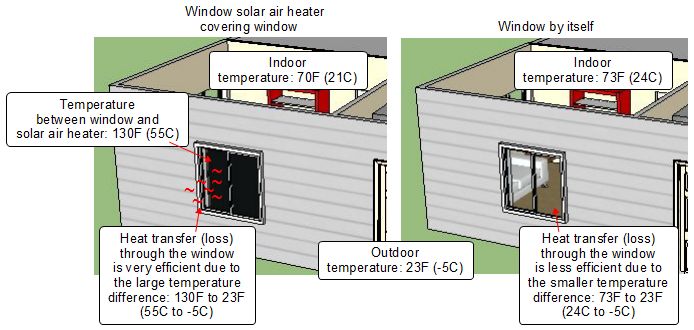
You can find out more about this, most often incorrect, use of a solar air heater on this page about window covering solar air heaters.

Normal wall

The examples given at the top of this page are for a wall. Keep in mind that a house wall is actually a little more complicated since it has windows, wooden studs, electrical boxes, ...

Assuming that none of these things overlap each other you simply take each object's surface area and divide it by the R-value for that object. This gives you the thermal conductance for each individual object. You then add up all the conductances and divide that total by the temperature difference.

For example, here are calculations for a simple 20 ft x 10 ft house wall with two windows.

Window R-value = 2
Window 1 area = 5 ft x 3 ft = 15 sq ft
Window 1 conductance = 15 / 2 = 7.5 BTU/hour x F
Window 2 area = 4 ft x 3 ft = 12 sq ft
Window 1 conductance = 12 / 2 = 6 BTU/hour x F

Wall R-vallue = 14
Wall area = (20 ft x 10 ft) - 15 sq ft - 12 sq ft = 173 sq ft
Notice that to get the area of just the wall material we subtracted the area taken up by the windows.
Wall conductance = 173 / 14 = 12.4

Outdoor temperature = 50F, Indoor temperature = 70F
Heat loss = (6 + 12.4) x (70 - 50) = 368 BTU per hour

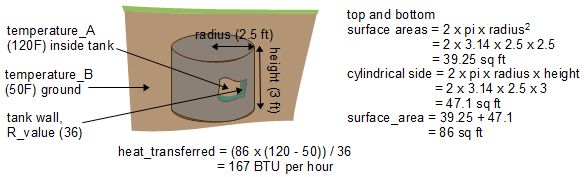
Underground tank

The temperature around 5 feet underground (or below the frost line) stays relatively constant throughout the year. As such it provides a constant temperature for a heat storage tank. In North America in many areas the temperature at that depth is around 40F to 50F, though it varies widely. The following are some sample calculations for a cylindrical container.