Backpropagation neural network software (3 layer)

This page is about a simple and configurable neural network software library I wrote a while ago that uses the backpropagation algorithm to learn things that you teach it. The software is written in C and is available and detailed below so that anyone can use it.

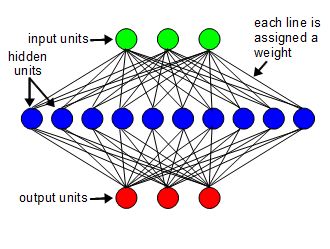
As shown in the diagram above, this software offers a simple, 2 layer neural network, which is fully connected. The two layers are the input layer, consisting of input units, and the output layer, consisting of output units. The hidden units don't count as a layer. The lines are all assigned values called weights. There are other components as well but those are not visible to users of the library, though you can see them if you look at the source code.

You choose how many input units, hidden units and output units there are. In the diagram above there are 3 input and 3 output units and 10 hidden units. For the sample program below there 3 input units, 4 hidden units and 3 output units. Saying that the network is fully connected means the each input unit is connected to every hidden unit and each output unit is also connected to every hidden unit. The connections are the lines.

The term backpropagation refers to the method used to train the neural network. Those details are hidden by the library, though you can see them if you download and examine the source code.

Video - Backpropagation Neural Network - How it Works e.g. Counting

This video demonstrates the counting neural network in action and also explains how the backpropagation algorithm works.

The neural network library

The library and sample program, testcounting, are written in C. You can try out the testcounting program or you can write your own code to use the neural network library to do something else.

The library and sample code consists of these files:

• testcounting.c or main.c - This contains main() and is sample code that uses the library to train the neural network to count and then tests it. If you're using the neural network for your own purposes then you won't need this file. Instead you'll create your own file with your own main() and make calls to the library in backprop.c to create and use a neural network. That structure and the function calls are described in detail below.
• backprop.c - This is the neural network library code. The sample code in testcounting.c uses this library.
• backprop.h - This is a header file that contains the needed data structures and function prototypes. You'll need an include line for this in whichever of your .c files uses the library.
• Makefile - Depending on what you download below there may be a makefile for making the executable.
• Other files depending on what you download below, such as project related files.

Downloading the library

Download - For building it using "make" from a console window/command line or shell

The following download is for building it and running it from a console window, command line or shell (e.g. a cygwin console window if you're using cygwin or a Command Prompt window in Windows Vista or or from a shell prompt in Linux.)

backprop.zip - 36KB

There is already a testcounter.exe executable in the archive that's been built and is ready to run. However, it's built to run under cygwin under Windows. If your environment or OS is different (e.g. you're using Linux) then run "make clean" first in order to remove the executable and object modules so that you can start building it from scratch from the source files.

You'll need a compiler like the GNU C compiler to build it. Simply go the the directory/folder where you've put the files and you should see the Makefile. Type "make" to build it.

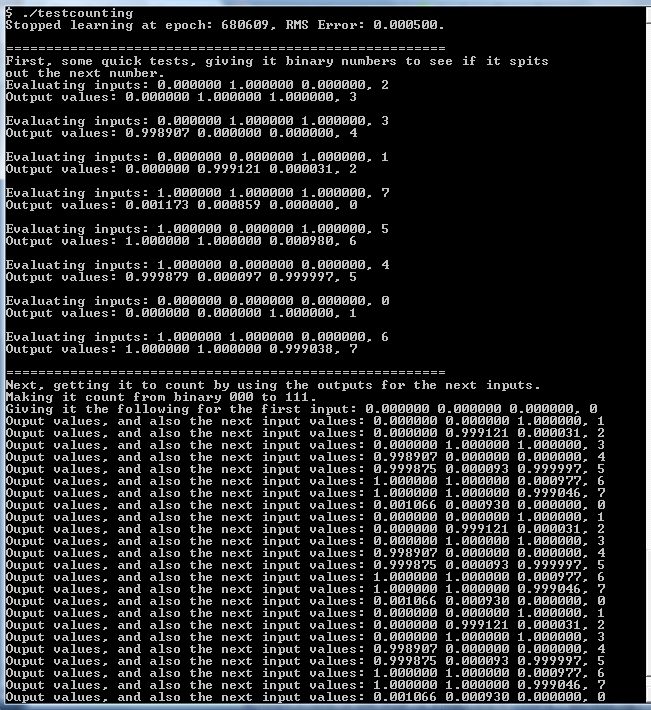
The following is a screen dump of the output of the testcounting sample program. It's run from a command line.

Download - For building it from CodeBlocks

The following download is a CodeBlocks project for building it from the CodeBlocks IDE. It was created in CodeBlocks as a "Console application" category of project.

testcounting_codeblocks.zip - 44KB

When you run it from within CodeBlocks it will run it in a console window (e.g. a Command Prompt window in Windows Vista.) That's because it is intended to run in a console type window. To run it outside CodeBlocks you'll need to run it in a console type window too. Once you've opened a console type window, change to the directory/folder that contains the executable (e.g. testcounting/bin/Release) and run testcounting. When running it you'll see the same sort of thing as the above screen dump.

In this project testcounting.c is called main.c instead.

Download - For compiling it under Visual Studio for Windows

The following contains a version for compiling under Visual Studio for Windows. In the .zip file you'll find a batch file called makevc.bat for a native compile.

backprop-vc.zip - 76KB

Thanks to James Brooks for supplying this.

Running the testcounting program

In the above screen dump, on the first line we run the program. Nothing happens briefly while the neural network is trained around 680,609 times, basically until its RMS error gets to below 0.0005 or 1,000,000 times, whichever happens first. In this case the RMS error got to below 0.0005 first. After the "=====..." the program does some quick tests to see how well the neural network can output the next binary value after having being given a binary value. For example, it's given a 2 and it outputs a 3. After doing a bunch more tests like that, not in numerical order, you then see another line of "=====..." followed by the fun test. In that test we simply give the neural network 0, which then causes it to output 1. We then take that 1 and blindly give it back to the neural network and it then outputs 2 (hopefully), and so on. The only input we chose for it though was the first 0. The rest of the numbers it came up with itself. i.e. it knew how to count to 7 and then back to 0 and then back to 7 and so on until the program decides to stop after having the neural network count to 7 three times.

You can also test saving the trained neural network to a file by running testcounting with the -s argument. It will save it to a file called testcounting_network.bkp. If using backprop.zip and running it from a command prompt then you'd run it as:

./testcounting -s

If using testcounting_codeblocks.zip then go to the Project menu, choose Set Programs' Arguments, and for the Release target, set the Program arguments to -s and then run it.

You can then test loading the trained neural network back in instead of having it do all the training by running testcounting with the -l argument. It will load it from the file called testcounting_network.bkp. If using backprop.zip and running it from a command prompt then you'd run it as:

./testcounting -l

If using testcounting_codeblocks.zip then go to the Project menu, choose Set Programs' Arguments, and for the Release target, set the Program arguments to -l and then run it.

The library functions

The following are the library functions:

int bkp_create_network(bkp_network_t **n, bkp_config_t *config)
void bkp_destroy_network(bkp_network_t *n)

int bkp_set_training_set(bkp_network_t *n, int ntrainset, float *tinputvals, float *targetvals)
void bkp_clear_training_set(bkp_network_t *n)
int bkp_learn(bkp_network_t *n, int ntimes)

int bkp_set_input(bkp_network_t *n, int setall, float val, float *sinputvals)
int bkp_set_output(bkp_network_t *n, int setall, float val, float *soutputvals)
int bkp_evaluate(bkp_network_t *n, float *eoutputvals, int sizeofoutputvals)

int bkp_query(bkp_network_t *n, 
   float *qlastlearningerror, float *qlastrmserror,
   float *qinputvals, float *qihweights, float *qhiddenvals, 
   float *qhoweights, float *qoutputvals,
   float *qbhweights, float *qbiasvals, float *qboweights)

int bkp_loadfromfile(bkp_network_t **n, char *fname)
int bkp_savetofile(bkp_network_t *n, char *fname)

Full descriptions of the parameters and return values are described just above each function in the backprop.c source file, though a lot is given below along with examples. All functions that return an int return 0 on success and -1 on failure, and with errno containing the error code as is common in C libraries.

Before using the library, you should first include the header file backprop.h. For example:

#include <backprop.h>

Creating the network

To use the library you first need to create the neural network. That's done by declaring and filling in a variable of type bkp_config_t. This is a structure for you to fill in.

typedef struct {
   short Type;
   int NumInputs;
   int NumHidden;
   int NumOutputs;
   float StepSize;
   float Momentum;
   float Cost;
} bkp_config_t;

Here are details about the above configuration parameters:

• Type - Set this to BACKPROP_TYPE_NORMAL (which is defined in backprop.h). Currently it's the only type supported.
• NumInputs - Number of input units.
• NumHidden - Number of hidden units.
• NumOutputs - Number of output units.
• StepSize - Also known as the learning rate. This is used to control the rate at which the weights between the units are changed. It should be between 0 and 1. If 0 is given then it defaults to 0.5.
• Momentum - Helps prevent the network from getting stuck in what are called local minima. It should be in the range 0 to 1. If a large Momentum is used then it's best to use a small StepSize. The Momentum's value is determined by trial and error. If -1 is given then it defaults to 0.5.
• Cost - A fraction of the weight's value to be subtracted from the weight itself whenever it's modified. Give 0 if not desired.

After filling in the bkp_config_t structure you then pass it to bkp_create_network() which creates the network and returns a pointer to it in the first argument you pass to bkp_create_network().

Note that bkp_create_network() also seeds the random number generator for the C rand() function with a different value each time it's called. It uses the return value from the time() function. This means the neural network's weights will have different random values each time a network is created, provided they're created at least 1 second apart since time() is guaranteed to return a different number only every second.

Example:

#define NUMINPUTS      3
#define NUMHIDDEN      4
#define NUMOUTPUTS     3
...
bkp_network_t *net;
bkp_config_t config;
...
config.Type = BACKPROP_TYPE_NORMAL;
config.NumInputs = NUMINPUTS;
config.NumHidden = NUMHIDDEN;
config.NumOutputs = NUMOUTPUTS;
config.StepSize = 0.25;
config.Momentum = 0.90;
config.Cost = 0.0;
if (bkp_create_network(&net, &config) == -1) {
   perror("bkp_create_network() failed");
   exit(EXIT_FAILURE);
}	

Training the neural network

Once created, you next want to train the neural network. The sample program below trains the neural network to count from 0 to 7 in binary. Once it's trained, if you give it three 0's for the input units (binary 000 is decimal 0) then it will output 0, 0 and 1 at the output units (binary 001 is decimal 1). If you give it 001 at the input then it will output 010, which is 2 in decimal. And so on.

To train it to do that you need to provide it with data called a training set. The training set is a set of inputs and their corresponding outputs. In the sample program they are defined as follows:

#define #define NUMINTRAINSET  8
...
float	InputVals[NUMINTRAINSET][NUMINPUTS] = {
	{ 0.0, 0.0, 0.0 }, 
	{ 0.0, 0.0, 1.0 }, 
	{ 0.0, 1.0, 0.0 }, 
	{ 0.0, 1.0, 1.0 },
	{ 1.0, 0.0, 0.0 },
	{ 1.0, 0.0, 1.0 },
	{ 1.0, 1.0, 0.0 },
	{ 1.0, 1.0, 1.0 }
};
float	TargetVals[NUMINTRAINSET][NUMOUTPUTS] = {
	{ 0.0, 0.0, 1.0 }, 
	{ 0.0, 1.0, 0.0 }, 
	{ 0.0, 1.0, 1.0 },
	{ 1.0, 0.0, 0.0 },
	{ 1.0, 0.0, 1.0 },
	{ 1.0, 1.0, 0.0 },
	{ 1.0, 1.0, 1.0 },
	{ 0.0, 0.0, 0.0 } 
};

InputVals above is an array of sets of values to be given to the input units. Notice that there are 3 values in each set, one for each input unit. TargetVals is a corresponding array that has the expected outputs for each input. Notice that the first set of input values is 0, 0, 0 and the first set of target values is 0, 0, 1, just as you'd expect given what I said in the paragraph above; for an input of binary 000 (decimal 0), the expected output is binary 001 (decimal 1).

To actually do the training you have two methods available.

The first is the simplest, call bkp_set_training_set(net, ntrainset, tinputvals, targetvals) passing it the pointer you got back from the call to bkp_create_network(), i.e. which network you're training, and then tell it how many sets of values are in the training set (8 in our example), and then the pointers to the two arrays.

Example:

if (bkp_set_training_set(net, NUMINTRAINSET, (float *) InputVals, (float *) TargetVals) == -1) {
   perror("bkp_set_training_set() failed");
   exit(EXIT_FAILURE);
}

That's then followed by a call to bkp_learn(net, ntimes) wherein you again pass it a pointer to the network to train and tell it how many times to repeatedly go through the training set, which you'd given the library through the called to bkp_set_training_set().

At that point, bkp_learn() will train the neural network by repeatedly giving it one set of input values and the corresponding set of target values, and then training it on those before moving on to the next pair and then after doing all 8, repeating the process again until it's repeatedly trained all 8 the number of times you specify in the ntimes argument you passed to bkp_learn().

Example:

if (bkp_learn(net, 1000000) == -1) {
   perror("bkp_learn() failed");
   exit(EXIT_FAILURE);
}

But waiting for the function to return after 1,000,000 iterations may be an issue. If you want more control then you can put it inside some sort of loop like the following:

int epoch, LastRMSError;
...
LastRMSError = 99;
for (epoch = 1;  LastRMSError > 0.0005  &&  epoch <= 1000000;  epoch++) {
   if (bkp_learn(net, 1) == -1) {
      perror("bkp_learn() failed");
      exit(EXIT_FAILURE);
   }
   bkp_query(net, NULL, &LastRMSError, NULL,
      NULL, NULL, NULL, NULL, NULL, NULL, NULL);
}

The the above code we have bkp_learn() go through the training set just once per call. Then we use bkp_query() to ask how well the training set has been learned by asking for the last RMS error it calculated. This is an error that should keep decreasing as more training is done. In the above loop we tell it to break out of the loop (i.e. stop training) when either the error has gotten to 0.0005 or the loop has iterated 1,000,000 times, whichever happens first.

Using the trained neural network

After you've trained the neural network you'll want to use it. To do that you give it some input and see what the output is. That's done by calling bkp_set_input() to set the input and then calling bkp_evaluate() to run the inputs through the neural network and get back the outputs.

Example:

static float TestInputVals[NUMOFEVALS][NUMINPUTS] = {
   { 0.0, 1.0, 0.0 }, 
   { 0.0, 1.0, 1.0 },
   { 0.0, 0.0, 1.0 }, 
   { 1.0, 1.0, 1.0 },
   { 1.0, 0.0, 1.0 },
   { 1.0, 0.0, 0.0 },
   { 0.0, 0.0, 0.0 }, 
   { 1.0, 1.0, 0.0 }
};
float ResultOutputVals[NUMOUTPUTS];
...
int j;
...
if (bkp_set_input(net, 0, 0.0, TestInputVals[4]) == -1) {
   perror("bkp_set_input() failed");
   exit(EXIT_FAILURE);
}
if (bkp_evaluate(net, ResultOutputVals, NUMOUTPUTS*sizeof(float)) == -1) {
   perror("bkp_evaluate() failed");
   exit(EXIT_FAILURE);
}
printf("Output values:");
for (j = 0;  j < NUMOUTPUTS;  j++)
   printf(" %f", ResultOutputVals[j]);

In the above example we have a selection of input values we can evaluate against with. In the call to bkp_set_input() we've chosen to give it the 5th one, which is { 1.0, 0.0, 1.0 } (in the C language, arrays count starting from 0, to so TestInputVals[0] is the 1st one and TestInputVals[4] is the 5th one.) We then call bkp_evaluate() which runs the neural network with the inputs we'd given to bkp_set_input() and then returns the resulting output in the array we'd passed, ResultOutputVals. Since our training set had taught it to count, we hope it gives us an output whose values are close to { 1.0, 0.0, 0.0 } which is binary 110 (decimal 6). That makes sense since the input was binary 101 (decimal 5).

Debugging the neural network

Getting a neural network to work well sometimes requires a few tricks, and trial and error. It also helps to be able to see what's going on inside the network, to see the values of the weights and the hidden units and how they change over time. That's where the bkp_query() function can help. Here's the prototype for bkp_query():

int bkp_query(bkp_network_t *n, 
   float *qlastlearningerror, float *qlastrmserror,
   float *qinputvals, float *qihweights, float *qhiddenvals, 
   float *qhoweights, float *qoutputvals,
   float *qbhweights, float *qbiasvals, float *qboweights)

Pass it the pointer to the neural network in the first parameter and pass it the address of suitable size buffers to the other parameters. Pass NULL for any ones you don't want. Here are all the parameters described:

• float *qlastlearningerror - The error for the last set of inputs and outputs learned by bkp_learn() or evaluated by bkp_evaluate(). It is the sum of the squares of the difference between the actual outputs and the target or desired outputs, all divided by 2.
• float *qlastrmserror - The RMS error for the last epoch learned i.e. the learning of the training set.
• float *qinputvals An array to fill with the current input values (must be at least bkp_config_t.NumInputs * sizeof(float)).
• float *qihweights - An array to fill with the current input units to hidden units weights (must be at least bkp_config_t.NumInputs * bkp_config_t.NumHidden * sizeof(float).
• float *qhiddenvals - An array to fill with the current hidden unit values (must be at least bkp_config_t.NumHidden * sizeof(float)).
• float *qhoweights - An array to fill with the current hidden units to output units weights (must be at least bkp_config_t.NumHidden * bkp_config_t.NumOutputs * sizeof(float)).
• float *qoutputvals - An array to fill with the current output values (must be at least bkp_config_t.NumOutputs * sizeof(float)).
• float *qbhweights - An array to fill with the current bias units to hidden units weights (must be at least 1 * bkp_config_t->NumHidden * sizeof(float)).
• float *qbiasvals - An array to fill with the current bias values (must be at least 1 * sizeof(float)).
• float *qboweights - An array to fill with the current bias units to output units weights (must be at least 1 * (*n)->NumOutputs * sizeof(float)).

Note that for the last three above, the size required is 1 * ... The reason for the 1 is because there is only one bias unit for everything. Theoretically there could be more though.

Example:

float LastLearningError;
float LastRMSError;
float ResultInputVals[NUMINPUTS]; 
float ResultIHWeights[NUMINPUTS*NUMHIDDEN];
float ResultHiddenVals[NUMHIDDEN];
float ResultHOWeights[NUMHIDDEN*NUMOUTPUTS];
float ResultOutputVals[NUMOUTPUTS];
float ResultBHWeights[1*NUMHIDDEN];
float ResultBiasVals[1];
float ResultBOWeights[1*NUMOUTPUTS];
...
if (bkp_query(net, &LastLearningError, &LastRMSError, ResultInputVals,
      ResultIHWeights, ResultHiddenVals, ResultHOWeights, 
      ResultOutputVals,
      ResultBHWeights, ResultBiasVals, ResultBOWeights) == -1) {
   perror("bkp_query() failed");
}
printf("RMS Error: %f  Learning Error: %f\nInput values: ", 
   LastRMSError, LastLearningError);
for (j = 0;  j < NUMINPUTS;  j++)
   printf("%f ", ResultInputVals[j]);

printf("\nInput to Hidden Weights: ");
for (j = 0;  j < NUMINPUTS*NUMHIDDEN;  j++)
   printf("%f ", ResultIHWeights[j]);

printf("\nHidden unit values: ");
for (j = 0;  j < NUMHIDDEN;  j++)
   printf("%f ", ResultHiddenVals[j]);

printf("\nHidden to Output Weights: ");
for (j = 0;  j < NUMHIDDEN*NUMOUTPUTS;  j++)
   printf("%f ", ResultHOWeights[j]);

printf("\nLast Outputs values for the last Epoch: ");
for (j = 0;  j < NUMOUTPUTS;  j++)
   printf("%f ", ResultOutputVals[j]);

printf("\nBias to Hidden Weights: ");
for (j = 0;  j < 1*NUMHIDDEN;  j++)
   printf("%f ", ResultBHWeights[j]);

printf("\nBias unit values: ");
for (j = 0;  j < 1;  j++)
   printf("%f ", ResultBiasVals[j]);

printf("\nBias to Output Weights: ");
for (j = 0;  j < 1*NUMOUTPUTS;  j++)
   printf("%f ", ResultBOWeights[j]);

printf("\n");

Saving the neural network to a file and loading it back again

You can also use bkp_savetofile() to have your program save the neural network to a file and use bkp_loadfromfile() to load it back again later, for example, the next time you run your program. The file format is raw data and not understandable as a human readable text file.

The prototypes are:

int bkp_savetofile(bkp_network_t *net, char *filename)
int bkp_loadfromfile(bkp_network_t **net, char *filename)

bkp_loadfromfile() will call bkp_create_network() for you and fill it with the information from the file. It will return the address of the already created and filled network in the pointer you pass it as the first argument.

Example:

if (bkp_savetofile(net, "testcounting_network.bkp") == -1) {
   perror("bkp_savetofile() failed saving to file testcounting_network.bkp");
   exit(EXIT_FAILURE);
}

Example:

if (bkp_loadfromfile(&net, "testcounting_network.bkp") == -1) {
   perror("bkp_loadfromfile() failed loading from file testcounting_network.bkp");
   exit(EXIT_FAILURE);
}

The file will contain the following with no separators between each item:

1. File format version e.g. 'A' (sizeof(char))
2. Network type BACKPROP_TYPE_* (sizeof(short))
3. Number of inputs (sizeof(int))
4. Number of hidden units (sizeof(int))
5. Number of outputs (sizeof(int))
6. StepSize (sizeof(float))
7. Momentum (sizeof(float))
8. Cost (sizeof(float))
9. Number of bias units (sizeof(int))
10. Is input ready? 0 = no, 1 = yes (sizeof(int))
11. Is desired output ready? 0 = no, 1 = yes (sizeof(int))
12. Has some learning been done? 0 = no, 1 = yes (sizeof(int))
13. Current input values (InputVals) (NumInputs * sizeof(float))
14. Current desired output values (DesiredOutputVals) (NumOutputs * sizeof(float))
15. Current input-hidden weights (IHWeights) (NumInputs * NumHidden * sizeof(float))
16. Previous input-hidden weight deltas (PrevDeltaIH) (NumInputs * NumHidden * sizeof(float))
17. Previous output-hidden weight deltas (PrevDeltaHO) (NumHidden * NumOutputs * sizeof(float))
18. Previous bias-hidden weight deltas (PrevDeltaBH) (NumBias * NumHidden * sizeof(float))
19. Previous bias-output weight deltas (PrevDeltaBO) (NumBias * NumOutputs * sizeof(float))
20. Current hidden unit values (HiddenVals) (NumHidden * sizeof(float))
21. Current hidden unit beta values (HiddenBetas) (NumHidden * sizeof(float))
22. Current hidden-output weights (HOWeights) (NumHidden * NumOutputs * sizeof(float))
23. Current bias unit values (BiasVals) (NumBias * sizeof(float))
24. Current bias-hidden weights (BHWeights) (NumBias * NumHidden * sizeof(float))
25. Current bias-output weights (BOWeights) (NumBias * NumOutputs * sizeof(float))
26. Current output values (OutputVals) (NumOutputs * sizeof(float))
27. Current output unit betas (OutputBetas) (NumOutputs * sizeof(float))

The sample program - Teaching a neural network to count in binary

The following is the sample program in full.

/*
 * testcounting.c - This program tests the neural network libary by
 * teaching it to count from 0 to 7 in binary.
 *
 * June 4, 2017 - Changed the number of hidden units from 3 to 4. This
 * is because when the backprop library was changed to seed the random 
 * number generator, the network would no longer always converge within
 * the maximum number of epochs in the loop below. With 4 hidden units
 * it now always converges, or at least for the all the times it's been
 * run.
 *
 * December 12, 2016 - Added -l option to demonstrate loading from a file,
 * and the -s option to demonstrate saving to a file.
 *
 * April 7, 2016 - Reduced the number of hidden units from 20 to 3.
 *
 * It structures the neural network with 3 inputs, 3 hidden layers
 * and 3 outputs.
 *
 * The 3 inputs represent binary digits and are each either 0 or 1.
 * Since there are 3 of them, that means they can represent:
 * 000, 001, 010, 011, 100, 101, 110, 111
 * which are the binary equivalents of the digital numbers:
 *   0,   1,   2,   3,   4,   5,   6,   7
 *
 * This program trains the network such that for the given input
 * 000, it should set the three output units to 001. For the given
 * input 001, it should set the three output units to 010 (which is
 * decimal is 2), and so on... The table of trained inputs to outputs
 * is below. The decimal equivalent is given in paranthesis.
 *  input   output
 * -------  -------
 * 000 (0)  001 (1)
 * 001 (1)  010 (2)
 * 010 (2)  011 (3)
 * 011 (3)  100 (4)
 * 100 (4)  101 (5)
 * 101 (5)  110 (6)
 * 110 (6)  111 (7)
 * 111 (7)  000 (0)
 *
 * This means that given any number from 0 to 6, in binary, it will
 * output the next highest number. The exception is 7, wherein it will
 * output 0. The cool thing is that if you give it 0 and from then on
 * just take its output and give it right back as the input for the next
 * time around, all the while displaying the outputs, it will count
 * from 0 to 7 and repeat continuously i.e. it will count.
 */
#include 
#include 
#include 
#include 
#include 
#include "backprop.h"

static int loadfromfile = 0;
static int savetofile = 0;
static int verbose = 0;

static void print_all_network_info(int epoch);
static int get_number(float *vals);
static int parse_args(int argc, char **argv);

#define NUMINPUTS      3 /* number of input units */
#define NUMHIDDEN      4 /* number of hidden units */
#define NUMOUTPUTS     3 /* number of output units */
#define NUMINTRAINSET  8 /* number of values/epochs in the training set */
#define NUMOFEVALS     8 /* number of values in the test set */

static float InputVals[NUMINTRAINSET][NUMINPUTS] = {
   { 0.0, 0.0, 0.0 }, 
   { 0.0, 0.0, 1.0 }, 
   { 0.0, 1.0, 0.0 }, 
   { 0.0, 1.0, 1.0 },
   { 1.0, 0.0, 0.0 },
   { 1.0, 0.0, 1.0 },
   { 1.0, 1.0, 0.0 },
   { 1.0, 1.0, 1.0 }
};
static float TargetVals[NUMINTRAINSET][NUMOUTPUTS] = {
   { 0.0, 0.0, 1.0 }, 
   { 0.0, 1.0, 0.0 }, 
   { 0.0, 1.0, 1.0 },
   { 1.0, 0.0, 0.0 },
   { 1.0, 0.0, 1.0 },
   { 1.0, 1.0, 0.0 },
   { 1.0, 1.0, 1.0 },
   { 0.0, 0.0, 0.0 } 
};
static float TestInputVals[NUMOFEVALS][NUMINPUTS] = {
   { 0.0, 1.0, 0.0 }, 
   { 0.0, 1.0, 1.0 },
   { 0.0, 0.0, 1.0 }, 
   { 1.0, 1.0, 1.0 },
   { 1.0, 0.0, 1.0 },
   { 1.0, 0.0, 0.0 },
   { 0.0, 0.0, 0.0 }, 
   { 1.0, 1.0, 0.0 }
};
float TestCountFromZero[NUMINPUTS] = {
   0.0, 0.0, 0.0,
};

float LastLearningError;
float LastRMSError;
float ResultInputVals[NUMINPUTS]; 
float ResultIHWeights[NUMINPUTS*NUMHIDDEN];
float ResultHiddenVals[NUMHIDDEN];
float ResultHOWeights[NUMHIDDEN*NUMOUTPUTS];
float ResultOutputVals[NUMOUTPUTS];
float ResultBHWeights[1*NUMHIDDEN];
float ResultBiasVals[1];
float ResultBOWeights[1*NUMOUTPUTS];

int
main(int argc, char **argv)
{
   int i, j, epoch;
   bkp_network_t *net;
   bkp_config_t config;

   if (parse_args(argc, argv) == -1)
      exit(EXIT_FAILURE);

   if (loadfromfile) {
      if (bkp_loadfromfile(&net, "testcounting_network.bkp") == -1) {
         perror("bkp_loadfromfile() failed loading from file testcounting_network.bkp");
         exit(EXIT_FAILURE);
      }
   } else {
      config.Type = BACKPROP_TYPE_NORMAL;
      config.NumInputs = NUMINPUTS;
      config.NumHidden = NUMHIDDEN;
      config.NumOutputs = NUMOUTPUTS;
      config.StepSize = 0.25;
      config.Momentum = 0.90;
      config.Cost = 0.0;
      if (bkp_create_network(&net, &config) == -1) {
         perror("bkp_create_network() failed");
         exit(EXIT_FAILURE);
      }

      if (bkp_set_training_set(net, NUMINTRAINSET, (float *) InputVals, (float *) TargetVals) == -1) {
         perror("bkp_set_training_set() failed");
         exit(EXIT_FAILURE);
      }

      LastRMSError = 99;
      for (epoch = 1;  LastRMSError > 0.0005  &&  epoch <= 1000000;  epoch++) {
         if (bkp_learn(net, 1) == -1) {
            perror("bkp_learn() failed");
            exit(EXIT_FAILURE);
         }
         if (verbose <= 1) {
            if (bkp_query(net, NULL, &LastRMSError, NULL,
                  NULL, NULL, NULL, NULL, NULL, NULL, NULL) == -1) {
               perror("bkp_query() failed");
            }
         } else  if (verbose == 2) {
            /* The following prints everything in the neural network for
               each step during the learning. It's just to illustrate
               that you can examine everything that's going on in order to
               debug or fine tune the network.
               Warning: Doing all this printing will slow things down
               significantly.  */
            if (bkp_query(net, &LastLearningError, &LastRMSError, ResultInputVals,
                  ResultIHWeights, ResultHiddenVals, ResultHOWeights, 
                  ResultOutputVals,
                  ResultBHWeights, ResultBiasVals, ResultBOWeights) == -1) {
               perror("bkp_query() failed");
            }
            print_all_network_info(epoch);
         }
      }
      if (verbose == 1) {
         /* The following prints everything in the neural network after
            the last learned training set. */
         if (bkp_query(net, &LastLearningError, &LastRMSError, ResultInputVals,
               ResultIHWeights, ResultHiddenVals, ResultHOWeights, 
               ResultOutputVals,
               ResultBHWeights, ResultBiasVals, ResultBOWeights) == -1) {
            perror("bkp_query() failed");
         }
         print_all_network_info(epoch);
      }

      printf("Stopped learning at epoch: %d, RMS Error: %f.\n",
         epoch-1, LastRMSError);
      printf("\n");
      printf("=======================================================\n");
   }

   printf("First, some quick tests, giving it binary numbers to see if it " 
      "spits\nout the next number.\n");
   for (i = 0;  i < NUMOFEVALS;  i++) {
      printf("Evaluating inputs:");
      for (j = 0;  j < NUMINPUTS;  j++)
         printf(" %f", TestInputVals[i][j]);
      printf(", %d\n", get_number(TestInputVals[i]));

      if (bkp_set_input(net, 0, 0.0, TestInputVals[i]) == -1) {
         perror("bkp_set_input() failed");
         exit(EXIT_FAILURE);
      }
      if (bkp_evaluate(net, ResultOutputVals, NUMOUTPUTS*sizeof(float)) == -1) {
         perror("bkp_evaluate() failed");
         exit(EXIT_FAILURE);
      }
      printf("Output values:");
      for (j = 0;  j < NUMOUTPUTS;  j++)
         printf(" %f", ResultOutputVals[j]);
      printf(", %d\n", get_number(ResultOutputVals));
      printf("\n");
   }	

   printf("=======================================================\n");
   printf("Next, getting it to count by using the outputs for the next inputs.\n");
   /* NOTE: Starting from 0.0, 0.0, 1.0 is better for some reason.
      0.0, 0.0, 0.0 -> 0.0, 0.0, 1.0 is not learned very well. */
   printf("Making it count from binary 000 to 111.\n");
   printf("Giving it the following for the first input:");
   for (j = 0;  j < NUMINPUTS;  j++)
      printf(" %f", TestCountFromZero[j]);
   printf(", %d\n", get_number(TestCountFromZero));
   if (bkp_set_input(net, 0, 0.0, TestCountFromZero) == -1) {
      perror("bkp_set_input() failed");
      exit(EXIT_FAILURE);
   }
   for (i = 0;  i < 3*NUMOFEVALS;  i++) {
      if (bkp_evaluate(net, ResultOutputVals, NUMOUTPUTS*sizeof(float)) == -1) {
         perror("bkp_evaluate() failed");
         exit(EXIT_FAILURE);
      }
      printf("Ouput values, and also the next input values:");
      for (j = 0;  j < NUMOUTPUTS;  j++)
         printf(" %f", ResultOutputVals[j]);
      printf(", %d\n", get_number(ResultOutputVals));
      if (bkp_set_input(net, 0, 0.0, ResultOutputVals) == -1) {
         perror("bkp_set_input() failed");
         exit(EXIT_FAILURE);
      }
   }

   if (savetofile) {
      if (bkp_savetofile(net, "testcounting_network.bkp") == -1) {
         perror("bkp_savetofile() failed saving to file testcounting_network.bkp");
         exit(EXIT_FAILURE);
      }
   }
   bkp_destroy_network(net);

   return 0;
}

static void print_all_network_info(int epoch)
{
   int j;

   printf("Epoch: %d  RMS Error: %f  Learning Error: %f\nInput values: ", 
         epoch, LastRMSError, LastLearningError);
   for (j = 0;  j < NUMINPUTS;  j++)
      printf("%f ", ResultInputVals[j]);
   printf("\nInput to Hidden Weights: ");
   for (j = 0;  j < NUMINPUTS*NUMHIDDEN;  j++)
      printf("%f ", ResultIHWeights[j]);
   printf("\nHidden unit values: ");
   for (j = 0;  j < NUMHIDDEN;  j++)
      printf("%f ", ResultHiddenVals[j]);
   printf("\nHidden to Output Weights: ");
   for (j = 0;  j < NUMHIDDEN*NUMOUTPUTS;  j++)
      printf("%f ", ResultHOWeights[j]);
   printf("\nLast Outputs values for the last Epoch: ");
   for (j = 0;  j < NUMOUTPUTS;  j++)
      printf("%f ", ResultOutputVals[j]);
   printf("\nBias to Hidden Weights: ");
   for (j = 0;  j < 1*NUMHIDDEN;  j++)
      printf("%f ", ResultBHWeights[j]);
   printf("\nBias unit values: ");
   for (j = 0;  j < 1;  j++)
      printf("%f ", ResultBiasVals[j]);
   printf("\nBias to Output Weights: ");
   for (j = 0;  j < 1*NUMOUTPUTS;  j++)
      printf("%f ", ResultBOWeights[j]);
   printf("\n\n");
}

/*
 * get_number - Given an array of three floating point values, each
 * in the range 0.0 to 1.0, this will convert any value <= 0.05 to
 * a 0 and any > 0.05 to a 1 and treat the resulting three 0s and 1s
 * as three binary digits. It will then return the digital equivalent.
 *
 * Example:
 * Given an array containing 0.00000, 0.94734, 0.02543, these will be 
 * converted to 0, 1, 0 or 010 which is a binary number that is 2 in 
 * digital. This will therefore return a 2.
 */
static int get_number(float *vals)
{
   int num = 0, i;

   for (i = 0; i < NUMOUTPUTS; i++)
      if (vals[i] > 0.05)
         num += 1 << ((NUMOUTPUTS-i)-1);
   return num;
}

static int parse_args(int argc, char **argv)
{
   int c;

   while ((c = getopt(argc, argv, "lsv")) != -1) {
      switch (c) {
      case 'l': loadfromfile = 1; break;
      case 's': savetofile = 1; break;
      case 'v': verbose++; break;
      case '?': exit(EXIT_FAILURE);
      }
   }
   if (argv[optind] != NULL) {
      fprintf(stderr, "Invalid argument.\n");
      return -1;
   }
   return 0;
}