Gravity light (v1) - Homemade/DIY
This is version 1 of my gravity light. A gravity light is a light (one or more LEDs) that is powered for a useful amount of time by a slowly falling object, or mass. In the photo below, my masses are two jugs containing a total of 8 liters/2.1 US gallons of water, and I'm using 3 LEDs as a reading light. The drop height is 2 1/2 feet/0.75 meters. Once the object has fallen all the way, you simply lift it back up and the light is lit again.
For more details and calculations see the main gravity light page.



This version ran for 8 minutes and produced just enough light to illuminate a book. Some problems were that:
- it had a short run of only 8 minutes,
- the light was bright enough to read by but could be improved,
- the stand leaned over too much in the direction of the heavy gravity light causing me to have to add a chain guide as a workaround to keep the chain from slipping off the sprocket.


Video - Gravity Light - a Homemade/DIY one (version 1)
This video gives an overview of the above homemade gravity light, the principle of how it works, and a demonstration of it in action.
Note that this video says the run time is 2 minutes but with the addition of a counterweight as shown in the next video below, along with a simple electrical circuit the run time is 8 minutes.
Video - Gravity Light - Making and Enhancements (version 1)
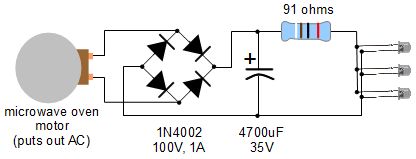
Here are step-by-step details for how I made the gravity light, as well as the simple addition of a counterweight that brought the run time from the 2 minutes reported in the above video to 4 minutes and the electrical circuit which brought it to 8 minutes. Since the microwave oven motor I'm using puts out AC, the circuit converts it to DC so that both halves of the cycle can be used. The capacitor smooths things out and the resistor gives the LEDs some protection. Note that 3 LEDs are now used. It's been suggested that using Schottky diodes in place of the 1N4002 diodes would be more efficient.