Gravity light - Homemade/DIY

A gravity light is a light (one or more LEDs) that is powered for a useful amount of time by a slowly falling object, or mass. In the photo below, my mass consists of containers of water, and I'm using LEDs as a reading lights. Once the object has fallen all the way, you simply lift it back up and the light is lit again.

This was invented by two fellows now working on it through a foundation called the GravityLight Foundation (formerly through Deciwatt) for selling cheaply to remote villages to use instead of kerosene lamps.

I decided to try making my own, and as you can see below, I succeeded.

The basic principle of the gravity light

As shown in the diagram below, the whole idea is to have the masses fall as slowly as possible, taking as long as possible, while still causing the generator to turn fast enough to power the LED light. With the system below, even though the small sprocket is turning slowly, the outer edge of the large pulley/wheel that it's attached to is turning fast and that's passed on to the generator.

It's in the use of the pulley system, along with that particular motor as a generator, that the conversion from slow to fast is done.

The generator I'm using is a motor from a microwave oven, the one that slowly turns the tray inside the oven (see the motor in the photos and the generator in the diagram.) If you turn the shaft of a motor manually then the motor acts as a generator and produces power. This motor has a lot of gears inside it, which make it such that turning the motor shaft slowly results in the magnets inside turning very fast, producing a useful amount of power. These motors are synchronous motors and normally run at 120 volts AC. All the ones I've seen are rated for 3 watts but their RPM varies from 2.5 RPM to 6 RPM.

My gravity light versions

So far I've made two versions of the gravity light.

Version 1

Version 1 ran for 8 minutes and produced just enough light to illuminate a book. The drop height was 2 1/2 feet/0.75 meters. Note that the dimensions for the wooden frame are given in a diagram below. Some problems were that:

• it had a short run of only 8 minutes,
• the light was bright enough to read by but could be improved,
• the stand leaned over too much in the direction of the heavy gravity light causing me to have to do a workaround to keep the chain from slipping off the sprocket.

Version 2

Verison 2 ran for 12 minutes and produced enough light to illuminate a book and some of the surroundings. The drop height was 4 feet/1.2 meters. Note that the dimensions for the wooden frame are given in a diagram below. Improvements over version 1 were:

• it ran for 12 minutes instead of 8, but this is still too short,
• the light was brighter and I'm not sure I can get it even more so,
• a new sturdy stand was made that fixed the leaning problem.

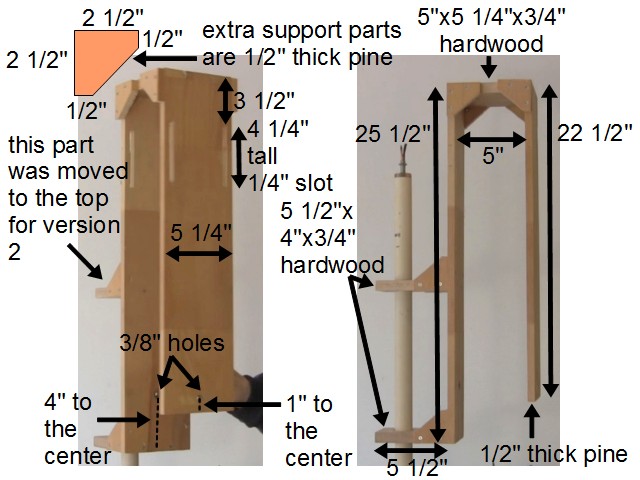
Wooden frame dimensions

Both version 1 and version 2 used the same wooden frame designed for a 25 inch diameter bicycle wheel (measured from rim to rim), though it can work with wheels with smaller diameter too. The dimensions are given below. The only critical dimensions are the size and positions of the holes that the bicycle wheel goes into and how far they are with respect to the 1/4" thick slots near the top (shown as 13 3/4" in the diagram).

Power and efficiency calculations

These are calculations done for the latest version of my gravity light, version 2, to get some idea of the efficiency.

Amount of falling water: 15.3 liters/4 US gallons
Distance it falls: 1.2 m (meters)/4 feet
Time is falls: 12 minutes

1 liter of water = 1 kg (kilogram)
15.3 liters was used, so that's 15.3 kg (kilograms) of water
15.3 kg x 9.8 m/s^2 = 149.94 N (Newton) weight or downward force here on Earth
149.94 N x 1.2 m distance = 180 J (joules)
180 J / (12 minutes x 60 seconds/minute) = 0.25 watts

I measured the voltage and current while the lights were lit.
Current: 2.7 millamps (0.0027 amps)
Voltage: 24 volts

power = current x voltage = 0.0027 amps x 24 volts = 0.065 watts
Note that the LEDs are rated at 10 watts, but the power available from the gravity light was nowhere near enough to run them at full power.

Comparing the two, (0.065 watts / 0.25 watts) x 100 = 26% efficiency. 26% is actually surprisingly good given what the losses must be in the bicycle wheel, the generator mounting bearings, the generator and the circuit.

Gravity light calculations

The following are the calculations I did to figure out if it would work given the things I had to work with.

The diagram above has Ar, Br and Cr added to it. These are the:

• rotational speed Ar of the small pulley A with the generator attached,
• rotational speed Br of the large pulley B, and
• rotational speed Cr of the small sprocket C that's attached to the large pulley.

I started with a generator, in this case actually a motor taken from a microwave oven. When you turn the shaft of a motor, the motor acts like a generator, producing electricity. I knew how fast I could turn it without damaging it and that it would be enough to light my LED. I had to turn it 1/2 turn each second.

I had a small pulley that I could attach to the generator shaft and its diameter is 1 inch, which is 25.4 mm (millimeters). To get the circumference of the pulley you simply multiply the diameter by the mathematical constant pi, which is 3.14159.

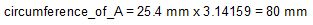
As I said above, I needed to turn it only 1/2 turn each second. That's a distance of 1/2 the circumference, so 1/2 of 80 mm is 40 mm. And I needed to turn it that distance every 1 second. That gives me the desired rotational speed of Ar as 40 mm/second.

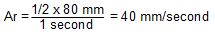
Now that I knew I needed a rotational speed for the small pulley of 40 mm/second (Ar), I needed to find some combination of large pulley with attached small pulley (or sprocket in this case), and possibly more than one of them that would cause a mass to fall at a reasonably slow speed for long enough to light the LED for a reasonably long time.

I had a bicycle wheel and made measurements of it to see if it would work. The bicycle wheel, which is my large pulley (B), is connected by belt to the small pulley (A). If the circumference of the small pulley is moving at a speed of 40 mm/second then the circumference of the large pulley is also moving at 40 mm/second. So Br is 40 mm/second.

The small sprocket (C) is pysically connected to the large pulley (B). A single turn of the large pulley results in a single turn of the small sprocket.

The circumference of the large pulley is 2010 mm and the circumference of the small sprocket is 157 mm. Since one turn of the large pulley means one turn of the small sprocket, that means when the large pulley goes 2010 mm, the small sprocket goes only 157 mm. The ratio of those two lengths is 0.078.

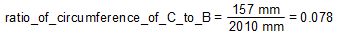
Since the rotational speed of the large pulley is 40 mm/second (Br), the rotational speed speed of the small sprocket is 3.1 mm/second, i.e. Cr is 3.1 mm/second.

That means that the mass will be falling at 3.1 mm/second. If the distance it has to fall is 1 meter, 1000 mm, then that will take 5.4 minutes.

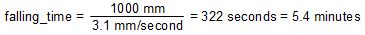
That means the calculated run time is 5.4 minutes, not taking into account losses, and assuming a reasonably sized mass can do it. As you'll see in the second video below on making the gravity light, I achieved an actual run time of 4 minutes using the bicycle wheel, 8 kilograms of mass and a 710 gram counterweight hanging from the other end of the chain.

Gravity light makers gallery

Here is a gallery of gravity light's made by others. Click on the images for larger versions.

If you'd like your homemade gravity light included here? Send me an email with a photo and how you want your name to be written, if at all, and I'll include it here. Also let me know any other details you want included such as why you made it (school project, for fun, for lighting something, ...), how long it runs for, how much weight you use, ...

Manjeet Singh's gravity light

Manjeet made this one for a school project and an exhibition.